什么是测度？What is Measure?

σ代数的定义：

σ代数又叫σ域，σ代数上可以定义测度。定义：设为集合。满足以下条件的集合系称为上的一个σ代数：
它的性质：σ代数是一个代数（域）也是一个λ系，它对集合的交、并、补、可列交、可列并运算都是封闭的，可测空间就是定义在一个σ代数上。

测度的定义：

数学上，测度(Measure)是一个函数，它对一个给定集合的某些子集指定一个数，这个数可以比作大小、体积、概率等等。传统的积分是在区间上进行的，后来人们希望把积分推广到任意的集合上，就发展出测度的概念，它在数学分析和概率论有重要的地位。测度论是实分析的一个分支，研究对象有σ代数、测度、可测函数和积分，其重要性在概率论和统计学中有所体现。
形式上说，一个测度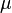（详细的说法是可列可加的正测度）是个函数。设是集合上的一个σ代数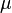，在上定义，于扩充区间中取值，并且满足以下性质：

空集的测度为零：
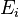可数可加性，或称σ可加性：若为中可数个两两不交的集合的序列，则所有的并集的测度，等于每个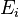的测度之总和：

这样的三元组称为一个测度空间，而中的元素称为这个空间中的可测集。